【CVPR '23】Learned Image Compression with Mixed Trasformer-CNN Architectures

Info

Title: Learned Image Compression with Mixed Transformer-CNN Architectures
Author: Jinming Liu
Pub: CVPR 2023
Repo: https://github.com/jmliu206/LIC_TCM
Keyword: Transformer, CNN

---

Motivation

1. 局部信息和全局信息都很重要。现有LIC基于Transformer或者CNN，它们有不同的优点，如何混合二者？在一个适当的复杂度如何获得更优的性能？
2. 现有的注意力模块可以关注到复杂区域，但是时间开销大，或者只关注到局部信息。
3. 现有模型在main或者hyperprior的path，这些path输入尺寸较大，因此计算复杂度也更高。

---

Method

Overview

1. 提出Transformer-CNN混合模块，将Transformer的全局建模能力和CNN的局部建模能力结合，且复杂度可接受。
2. 设计通道级的自回归熵模型：提出参数高效的机遇Swin-Transformer的注意力模块SWAtten。只做通道级的，相较于其它lic输入尺寸只有1/16.

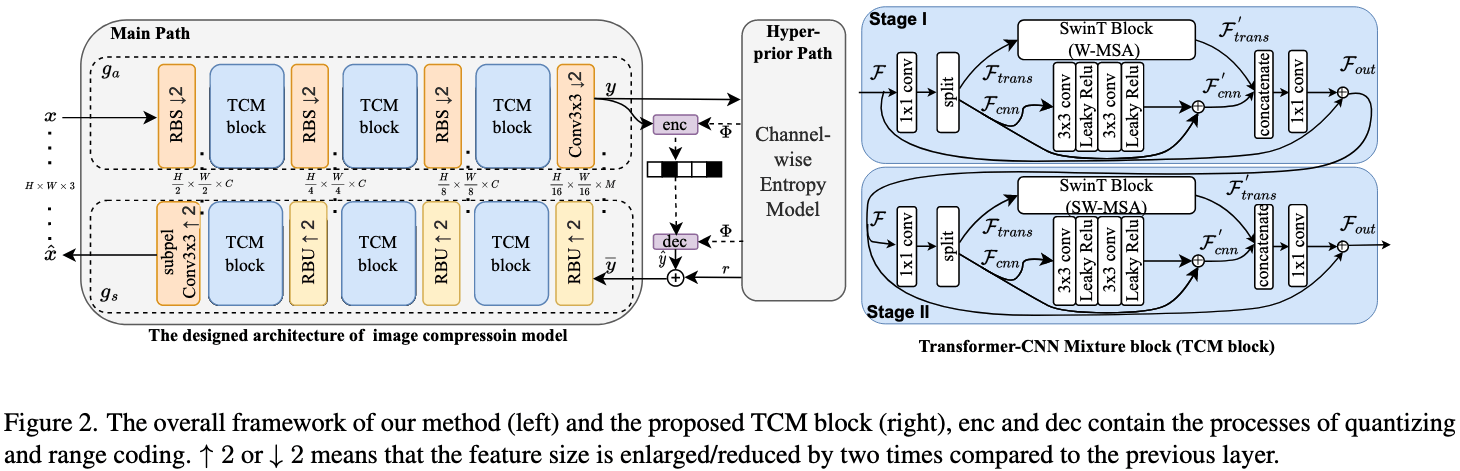主要改进由两部分：变换网络和熵建模，均是将Transformer与CNN进行结合。

对变换Encoding和Entropy Model进行了改进。变换是提出了TCM block，提取特征，将局部和全局混合起来。Entropy Model是通道级别的。 通过超先验捕捉潜像的统计特性，再将潜像切片处理实现自回归编码。

因此Transformer与CNN的结合包含两部分：变换网络和熵建模

变换网络：TCM-Block

TCM：将Residual Networks (CNN) 和Swin-Transformer blocks （Transformer）结合，实现全局和局部信息的综合建模能力。
1. 输入从通道级别拆分长两部分，然后分别输入到CNN和Transformer模块进行处理，然后再通过Conv1融合局部和非局部特征。从通道级拆分的好处：减少特征通道的数量，以减少复杂度。并且局部和全局可以独立同时处理。 2. 两个相似阶段构成，stage1，使用window-based多头自注意力，stage2，使用shifted window-based 多头自注意力。这样残差网络可以嵌入到两个连续的SWtrans中，更有效的特征融合。 TCM block在framework是在main path替代了现有算法的GDN。剩余的Conv变成了带有残差的下采样和上采样块。 3. 用了有效感受野（ERF）验证了TCM的核心优势：同时兼顾CNN的局部信息捕捉能力和Transformer的非局部信息建模能力。

熵模型

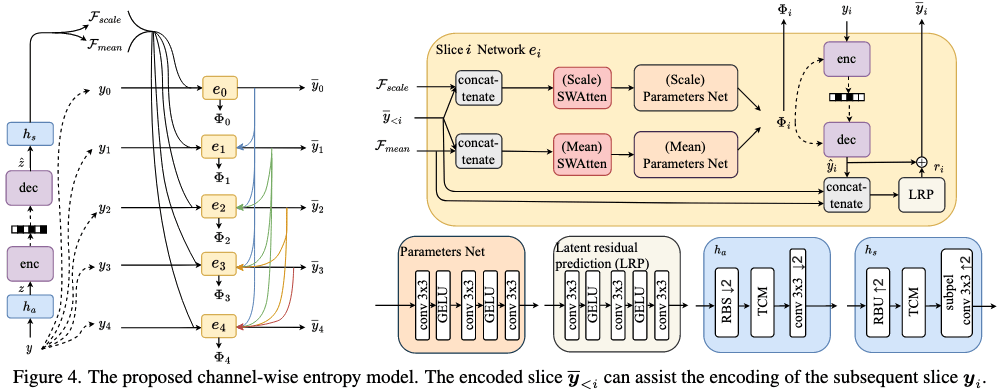为熵模型设计了尺寸仅为Main Path的1/16的基于Swin-Transformer的注意力模块SWAtten。 上下文这里采用了“基础特征+累积上下文”。即： $ M+i(M//s) $ SWAttten：结合SwinT block（非局部信息），与残差块（局部信息）。

SWAtten与变换网络均采用Transformer和CNN混合构成。但二者区别是：
1）超先验路径包含大量荣誉参数，可以通过通道压缩操作减少参数量。
2）SWAtten的CNN不仅提取局部特征，还用于提取注意力maps。
3）SWAtten所在的熵模型感受野已足够大，无需采用TCM的双阶段设计。

渐进式熵模型的示例： 设y分割为 n 个slice：{y₀, y₁, ..., y_n − 1}，从ẑ解码出来的均值和方差分别为 means 和 scales。
以解码 y₂ 为例：
1. 将 means 与[ŷ₀, ŷ₁]拼接。 # 最多参考5个
2. 经过 e₂ 得到 μ₂
3. 将 scales 与[ŷ₀, ŷ₁]拼接
4. 经过 e₂ 得到 σ₂
5. ŷ₂ = GaussianConditional(y₂, μ₂, σ₂)
6. 然后循环，直到最后 y_n − 1解码完成

---

Experiment

Dataset

Train Sets：ImageNet中随机300k个短边大于等于256的图像。
Test Sets：Kodak，Tecnick，CLIC validation。
Metrics：PSNR，MS-SSIM，bpp
Baselines：VTM，Hyperprior，Cheng2020，Xie，Chen，He。
算法分为small，medium，large三种模式，对应了中间层channel的数量（分别是128，192，256）。本文对比是用的Large模式。

Result

从重构效果来看，要比当时的Sota要好。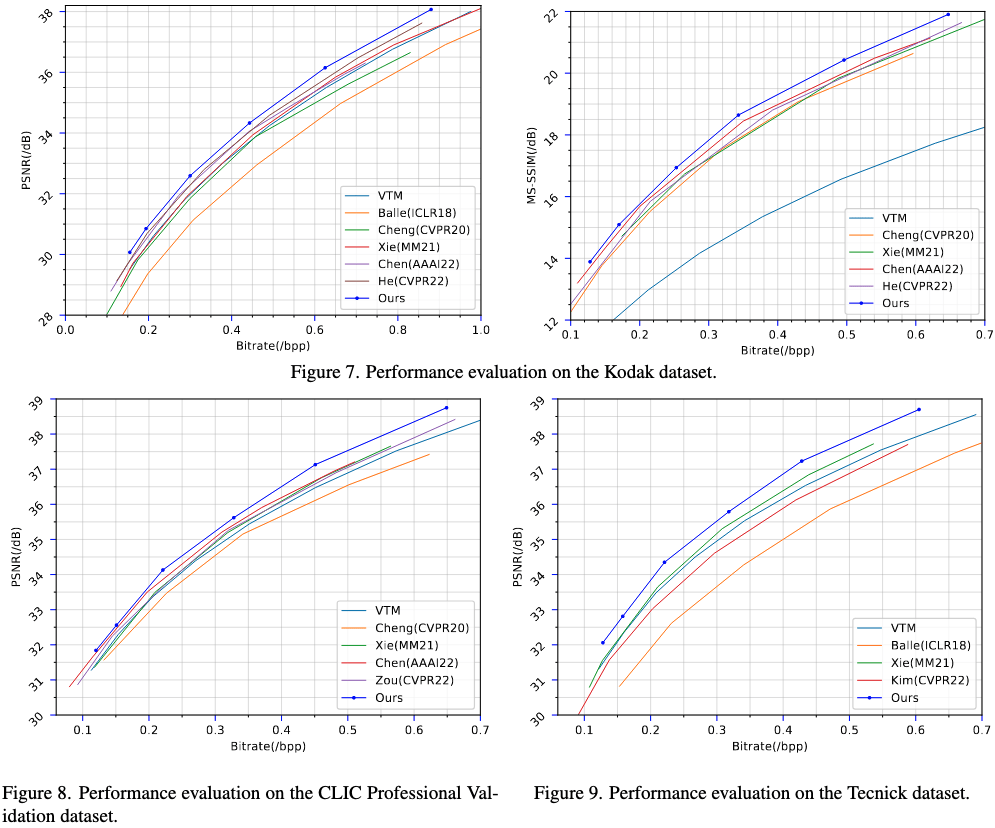

从Encoding和Decoding的时间上，要优于Xie。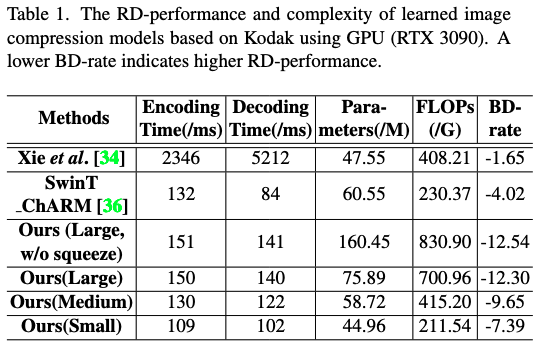

---

Discussion

作者将Transformer和CNN的优势相结合。同时尽量避免了模块叠加所带来的复杂度飙升问题。二者的结合不仅用于Encoding阶段，还有后面的Entropy Coding阶段。且两个阶段的组合方式也有区别。 工作提供了详细的代码，但是仓库只提供了C=64的6个模型和C=128的一个模型，并不是文中的Large模型，但是也可以作为Baseline。有条件的可以自己训练一组。

---

Note

1. Summary: Balle 首先提出End-to-End的CNN-based可学习压缩模型。接着提出VAE和Hyperprior。Cheng 提出了使用残差网络；Chen提出octave residual networks；Xie提出Invertible Neural Networks（INNs）。Zhu[36]和Zou[37]构建Swin-Transformer的LIC。 Qian[28]使用ViT。Koyuncu使用sliding window，减少ViT的复杂度。Kim提出Information Transformer获取全局和局部信息。Liu[21]首次引入非局部注意力模块，但耗时。
2. 对 ⌈y − μ⌋取整并编码为比特流，而非对y直接取整；同时将ŷ重构为⌈y − μ⌋ + μ，对熵模型带来增益。 本质上是中心量化，μy的估计均值（由通道级伤模型推导而得）。这里的μ是Entropy Model得出的，对应的还有Scale。
3. 熵编码阶段，连续型变量的概率密度函数->离散型变量的概率质量分数 $$ p_{\hat{z} | \psi}(\hat{z} | \psi) = \prod_{j}\left(p_{z_j | \psi}(\psi) * \mathcal{U} \left(-\frac{1}{2}, \frac{1}{2}\right)\right)(\hat{z}_j) $$ p_ẑ|ψ(ẑ|ψ)是给定参数ψ下的变量ẑ的整体概率质量函数。 p_zj|ψ(ψ) 是由因子化密度模型参数ψ估计的、z_j的连续概率密度函数，描述z_j在连续数值域的概率分布。 $\mathcal{U} (-\frac{1}{2}, \frac{1}{2})$表示在区间$[-\frac{1}{2},\frac{1}{2})$上的均匀分布，即概率密度值恒为1. Exp: 两个PDF卷积后得到PMF的核心原因是：卷积操作本质是计算连续变量在量化间隔内的累积概率，而该累积概率恰好对应离散量化变量的概率值，是概率论中“连续概率转离散概率”的标准方式。本质上是计算z_j落在ẑ_j = k对应区间$[k-\frac{1}{2},k+\frac{1}{2})$的概率，结果即为ẑ_j = k的PMF，即为 $$ (p_{z_j | \psi}(\psi) * \mathcal{U} (-\frac{1}{2}, \frac{1}{2}))(\hat{z}_j) $$ 假设量化后ẑ的不同元素ẑ_j相互独立，因此ẑ的整体概率等于各元素概率的乘积。即 $$ p_{\hat{z} | \psi}(\hat{z} | \psi)= (p_{z_1 | \psi}(\psi) * \mathcal{U} (-\frac{1}{2}, \frac{1}{2}))(\hat{z}_1) \times ... \times (p_{z_N | \psi}(\psi) * \mathcal{U} (-\frac{1}{2}, \frac{1}{2}))(\hat{z}_N) $$