【CVPR '25】Learned Image Compression with Dictionary-based Entropy Model

Info

Title: Learned Image Compression with Dictionary-based Entropy Model
Author: Jingbo Lu
Pub: CVPR 2025
Repo: https://github.com/LabShuHangGU/DCAE
Keyword: Dictionary-based, Cross Attention

---

Motivation

现有算法大多采用Hyperprior和自回归架构建立熵模型，仅仅探索了潜在表示（latent represent）的内部依赖性，而忽视了从训练数据中提取prior的重要性。

Hyperprior Architecture

---

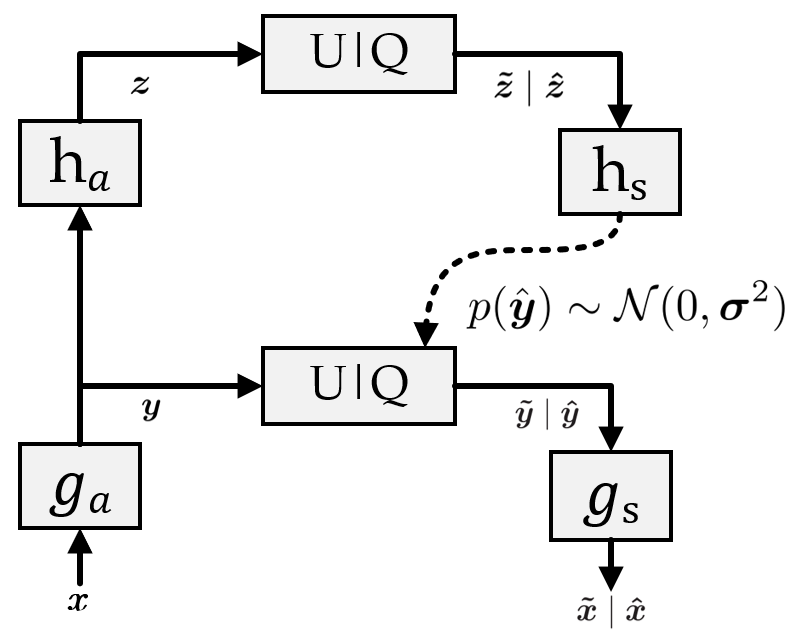
Method

本文没有进一步探索内部依赖性，而是提出基于字典的交叉注意力熵模型（Dictionary-based Cross Attention Entropy，DCAE），试图从训练数据中获取prior。先看一下算法的整体框架：

Fig.1 Over Architecture

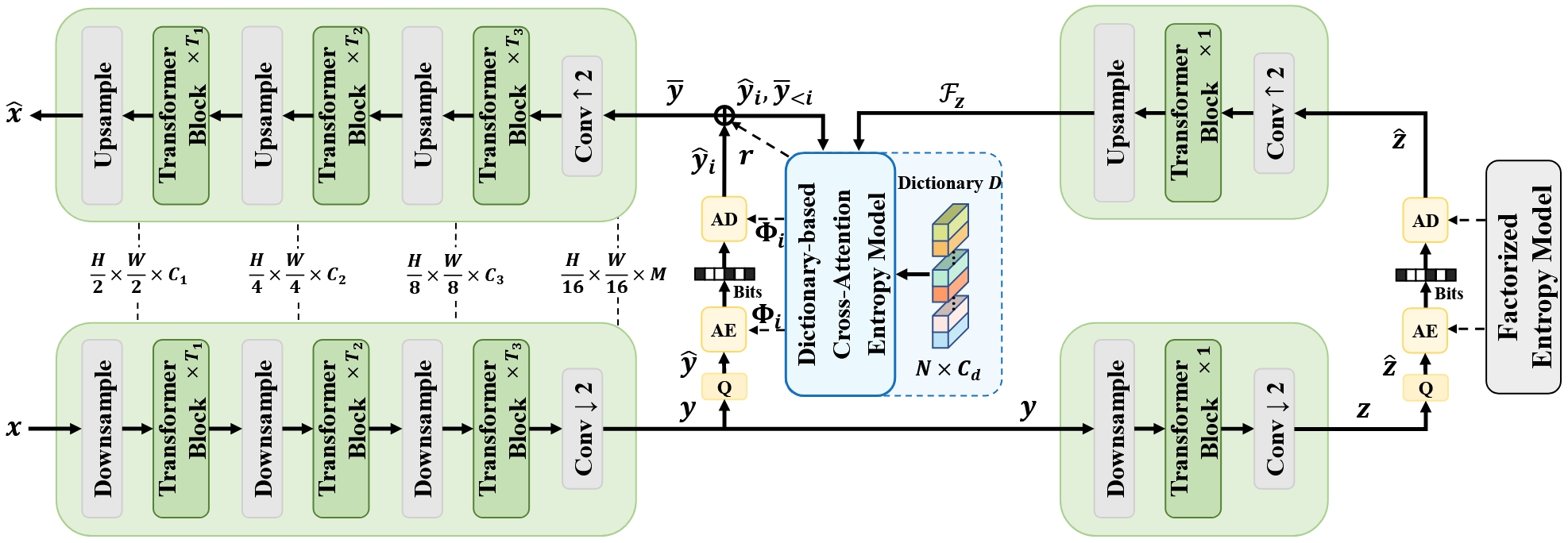
作者提出的DCAE模型根据潜在表示y来计算分布参数Φ，以结合熵编码算法（Entropy Coding， AE）无损压缩到比特流。所以左边Encoder和Decoder非线性变换就不细讲了，作者给出了具体的结构图，可以参考原文。下面就主要看一下DCAE部分：

Fig.2 DCAE

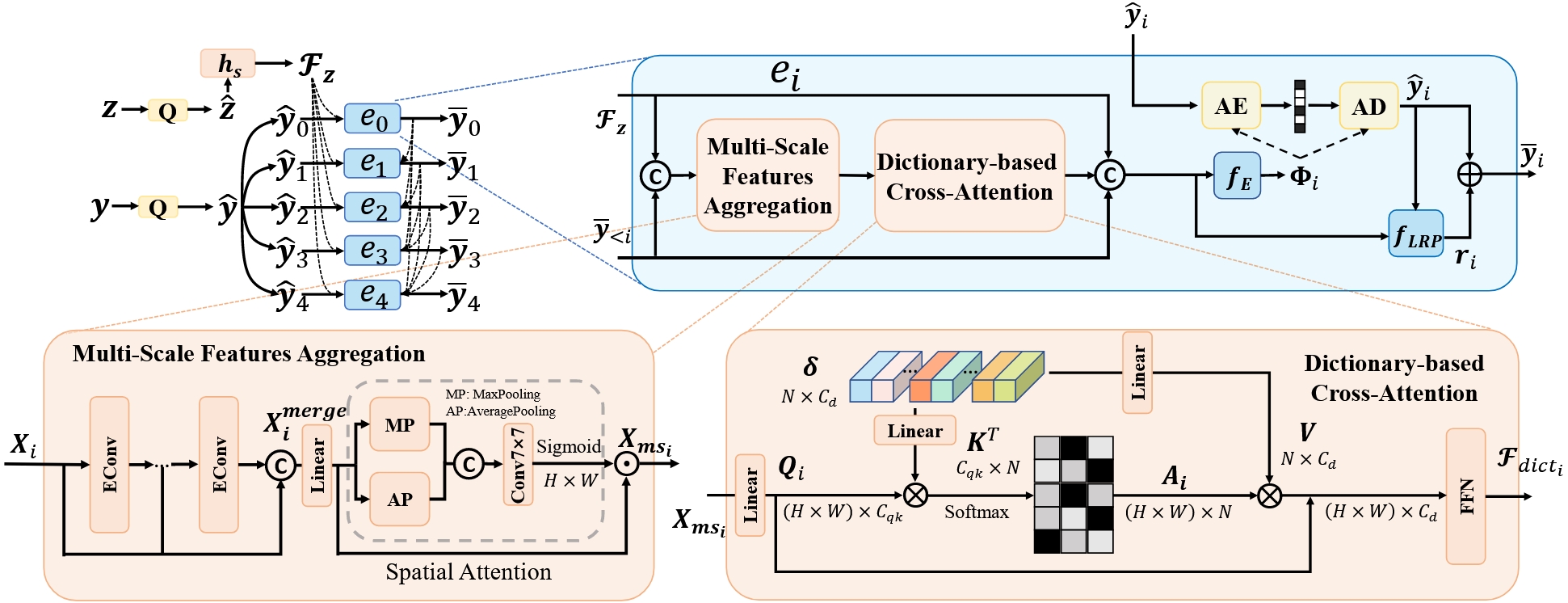
从左上角开始看，y经过量化后得到ŷ，然后就是Minnen 2018工作提出的自回归架构，即将ŷ分割为多个片段{ŷ₀, ..., ŷ_s − 1}。其中完成解码的ȳ_< i去指导后一个片段ŷ_i的编码和解码，见右上角的输入输出。（这里编解码是Φ和AC结合实现压缩的步骤，而非最开始图像和y之间的变换过程）

左下的多尺度特征聚合模块。输入X_i = [ℱ_z, ȳ_< i]，其中ℱ_z是Balle 2018提出的Hyperprior中的概念，这里可以理解为包含空间依赖信息的全局特征。接着右边的基于字典的交叉注意力也不难理解，最终输出ℱ_dicti。

最后分布参数Φ_i = {μ_i, σ_i} = f_E(ℱ_z, ȳ_< i, ℱ_dicti)， 量化误差r_i = f_LRP(ℱ_z, ȳ_< i, ℱ_dicti, ŷ_i)， 去掉ℱ_dicti就是原版的Hyperprior。

---

Experiment

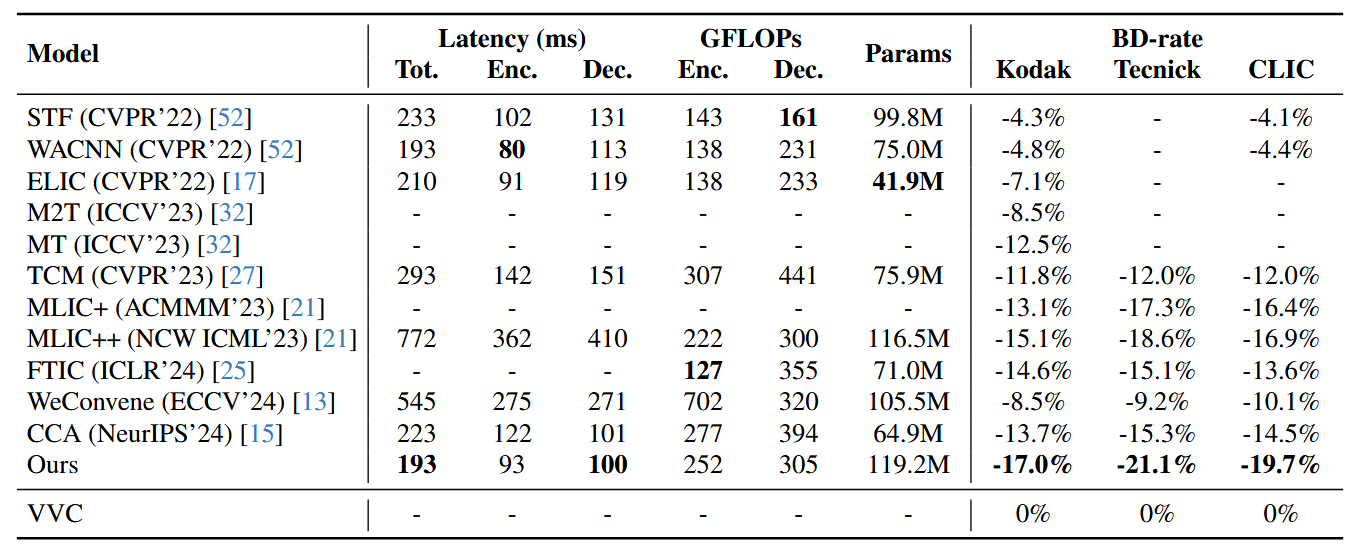
训练： Openimages 测试： Kodak，Tecnick Testset，CLIC。Baselines的结果由作者论文提供。 结果： 先看效果，三个数据集上的PSNR都达到了SOTA。

Fig.3 PSNR-bpp

再看效率，以VVC为基准，BD-rate和Latency最优。缺点就是参数量相较于其他算法最大。

Fig4. Model perfermance

---

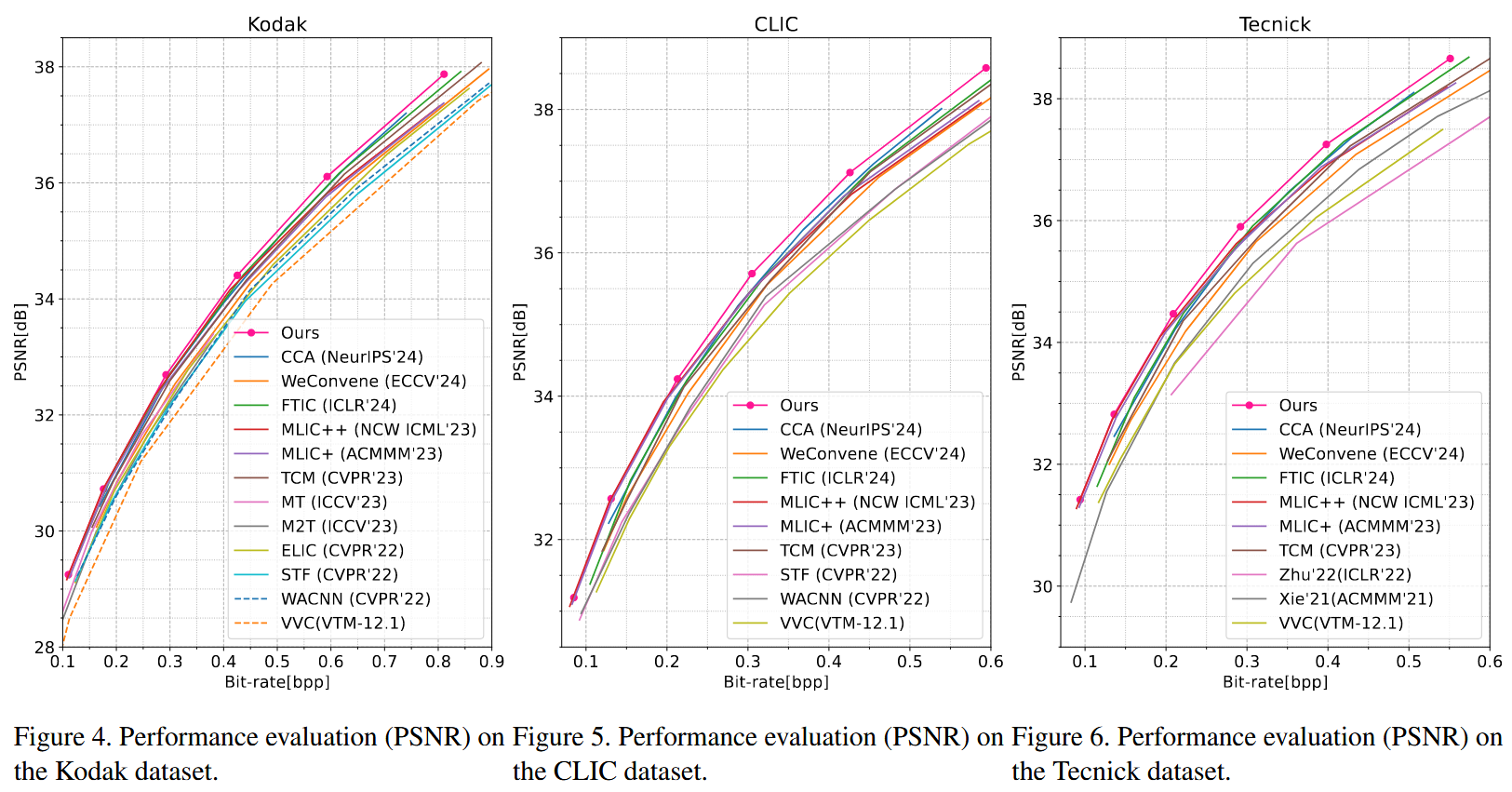
Discussion

作者提出的DCAE模型，从训练集中获取先验，压缩时直接从字典中找到相似模板来匹配。

这里很像JPEG算法中离散余弦变换，通过频域变换将图像分解为一组标准频率分量的加权和。可以简单理解为一组有限个标准模板，通过堆叠可以组合成任意图像。

略读了一遍，太多细节可以见论文。后续有时间来把更多细节补上。

---

Note

1. 可学习图像压缩（Learned Image Compression, LIC)包括两个关键部分：可学习非线性变换和熵模型。 可学习非线性变换：编码器和解码器是将图像和潜在表示相互转换。即将图像转换为适用于熵编码的紧凑的潜在表示，或将潜在表示重建回图像。 熵模型：用于预测潜在表示的分布参数，以结合熵编码算法实现压缩。
2. 一类算法（例如Cheng 2020）探究了先进的自动编码器结构，以建立更准的潜在表示提取器（改进前者），而另一类算法（例如Balle 2018）更关注熵模型本身，以优化码率和失真之间的权衡。
3. 熵模型的核心是分布估计器（estimator），例如Fig.2的f_E（Factorized Entropy Model）。
4. 可学习非线性变换的发展可分为两类：基于CNN和基于Transformer。
5. 中心化量化：ŷ = ⌈y − μ⌋ + μ，减去均值（中心化）→四舍五入（量化）→加上均值（反中心化，减少重建误差）。相较于直接量化误差更小，也就是更不失真。